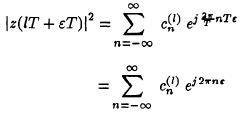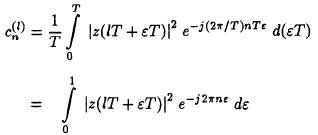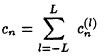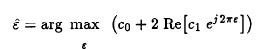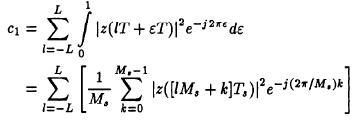Timing Recovery:

Introduction

2 Basic Functions for Digital Timing Recovery

Optimum ML Receivers

Derivation of Synchronization Algorithm

1.NDA

2.NDA by Spectral Estimation

3.DD(DA)

4.Timing Error Feedback Systems at Symbol Rate

NDA Timing Parameter Estimation by Spectral Estimation

           Consider the following objective function:
           
                                               
           assume a  symmetric observation interval [-L, L].For a sufficiently large
           number N of transmitted symbols (N >> L) the process ]z( IT + ET) I2 is 
           (almost) cyclostationary in the observation interval. A cyclostationary
           process has a Fourier series representation:

where the coefficients are random variables defined by:

as a consequence we have:

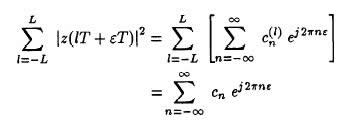
where:

It is proved only three coefficients {c-1,c0,c1} have nonzero mean hence if
L(ε) is approximated with its average clearly :

and this results in:

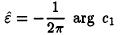
Although this approach solve the problem of maximum search algorithms ,
only digital algorithms are of interest here while c1 is defined by a summation of
(2L+1) integrals, but provided the sampling rate l/T, is such that the sampling theorem
is fulfilled for |z(t)|^2 [and not only for z(t)], i.e. :

the coefficients c1, c0 can be computed by a discrete Fourier transform (DFT).
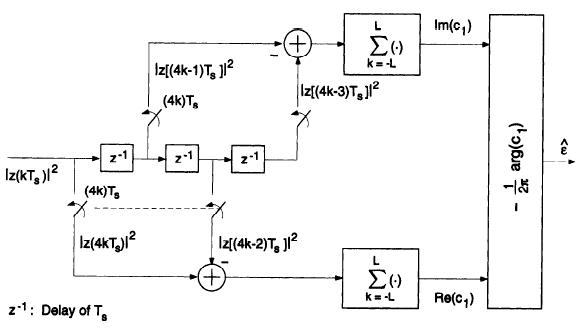
Let us denote by the integer Ms the (nominal) ratio between sampling and symbol
rate, Ms = T/Ts. For the samples taken at kTs:

The following figure illustrates a simple implementation for Ms=4:

 

Three following methods based on this spectral estimation with an itterative
algorithm figure on finding timing estimation (ε):


1. Early-late gate
2. Gradient-based
3. Tone-extraction
about which there are more details in "Signal Processing Techniques
for Software Radio " Book , Behrouz Farhang-Boroujeny,chapter 10 .

home

shima_kheradmand@yahoo.com