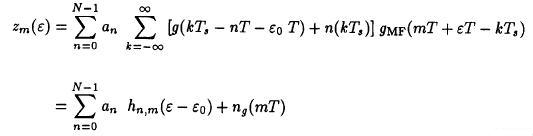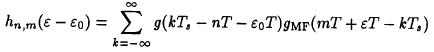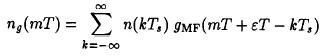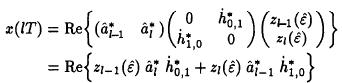Timing Recovery:

Introduction

2 Basic Functions for Digital Timing Recovery

Optimum ML Receivers

Derivation of Synchronization Algorithms :

1.NDA

2.NDA by Spectral Estimation

3.DA(DD)

4.Timing Eroor Feedback Systems at Symbol Rate

.

Timing Error Feedback Systems at Symbol Rate

There are error detector algorithms (both DA and NDA) whereby timing can be recovered from the T-spaced samples of the analog receiver filter which need not necessarily be a matched filter. The sampling instant is controlled by a numerically controlled oscillator (NCO).If the matched filter is realized digitally,there is no way around using the higher sampling rate l/Ts to satisfy the sufficient
statistic conditions. Sampling at symbol rate l/T does not provide the information required for timing recovery.

This algorithm is derived from analog matched filter outputs. The matched filter output z(mT + εT) equals:

.

             (1)

in which the (phase-corrected) received signal is:

        (2)

Notice that we distinguish between the true (unknown) parameters (ε0, θ0) and the
trial parameters (ε, θ) in the last two equations. In the sequel we assume that an
accurate phase estimate θ is available, thus : 

Inserting the right-hand side of last eq. into eq.(1) yields:
                      

where hn,m(ε-ε0) is defined as
                  

For a symmetric prefilter F(w) it was shown that the noise process:
                      

is white.Now a log-likelihood function for the samples
 {z(nT)}  over the L-sample segment can be written:

                          

             (3)
            

                           
 eliminating all terms irrelevant to optimization from (3), we obtain objective function:

                              

               (4)
           

The error signal is obtained by differentiating (4) with respect to ε and
evaluating the function at ε = ε:

              (5)

A class of particularly important algorithms can be derived from the third line of
(5) which works with T-spaced samples of the matched filter, while the first
two lines require suitable approximation of the derivative z(mT +εT). We thus
neglect the first two lines of (5). Doing so we later will have to verify that
this approximation indeed leads to a working timing error signal.
Since we are concerned with an error feedback system, only estimates ε close
to the true values are of interest. We thus approximate:

For simplicity we use the simpler notation 
 from now on. 
Hence, the error signal at time 1 for the L samples from l - (L - 1) to l becomes:

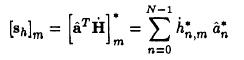
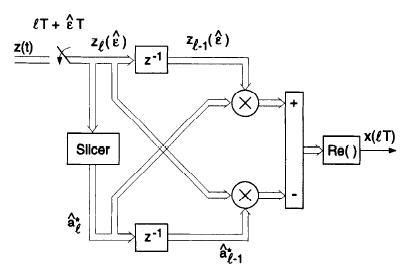
in which for L=2 yields:
                                                      

For a real pulse g(t) :

and these two entries are real, hence:
                                                          

This algorithm was first proposed by Mueller and Müller in their seminal paper
and has been widely used in telephony modem applications.

                                                                

      Mueller and Müller Algorithm

home 

shima_kheradmand@yahoo.com