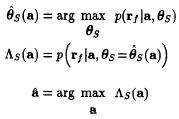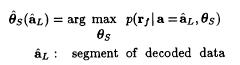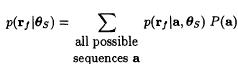Isfahan University of Technology
Software Radio Course Project ( spring-summer 2007)
Shima Kheradmand
Timing Recovery:
2 Basic Functions for Digital Timing Recovery
Optimum ML Receivers
Derivation of Synchronization Algorithms :
4.Timing Error Feedback Systems at Symbol Rate
Optimum ML receivers
The ultimate goal of a receiver is to detect the symbol sequence a in a received
signal disturbed by noise with minimal probability of detection error. It is known
that this is accomplished when the detector maximizes the a posteriori probability
for all sequences a
We can rewrite the a posteriori probability using Bayes’s rule:
For equally probable data sequences then maximizing the a posteriori probability is the same as maximizing the likelihood function p(rf|a). We notice that the synchronization parameters are absent.As far as detection is concerned they must be considered as unwanted parameters which are removed by averaging. At next step assume the receiver operates at high signal-to-noise ratio, then the
likelihood function weighted by the a priori probabilities becomes concentrated at its maximum:
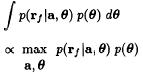
Maximizing the integral leads to the rule:
As a first important result we observe that the receiver performs a joint detection/
estimation. There is no separation between synchronization and detection
units. At this point it is necessary to take a closer look at the properties of the
synchronization parameters. In particular we have to distinguish between parameters
which are essentially static, es, and parameters that may be termed dynamic,
80. For static parameters there is no useful probabilistic information except that
they are in a given region. Therefore, θs is unknown but nonrandom.the joint detection/estimation thus reduces to maximizing the likelihood function p(rf |a, θs) with respect to (a, θs):
On the other hand, probabilistic information is availablefor dynamic parameters and
should be made use of. Hence joint detection and estimation calls for maximizing
We continue on with assumption static parameter estimation. Since there are infinitely many possible values of the synchronization parameters
while the number of possible sequencesis finite, the most naturalj oint maximization
procedure is to first maximize the joint likelihood function p(rf la, θs)
with respect to θs for each possible a and then select the sequence a with the
largest likelihood:
sequence. Clearly,this optimum joint estimation detection rule is far too complex for a practical application. A first approacht o separate the joint detection estimation rule into two disjoint
tasks is to transmit a preamble a0 of known symbols prior to sending the useful
data. During the preamble the (static) synchronization parameters can be estimated.
The estimation rules which use a known sequence a0 are called data-aided(DA).
Subsequent detection of the useful data a is then done using the estimate θs(a0)
as if it were the true value:
In order to accommodate ever-presents low variations of the synchronization
parameters one may use segments of the decoded sequence to update the synchronization parameter estimate:
Another possibility is to actually perform the averaging operation to remove
the data dependency:
This results in the class of non-data-aided (NDA) synchronization algorithms,
and finally:
Hence the only remained problem is Systematic derivation of synchronizartion algorithms. homeshima_kheradmand@yahoo.com