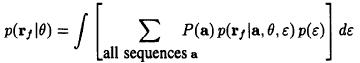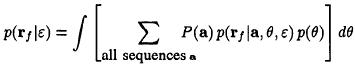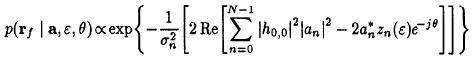Isfahan University of Technology
Software Radio Course Project ( spring-summer 2007)
Shima Kheradmand
Timing Recovery:
2 Basic Functions for Digital Timing Recovery
Derivation of Synchronization Algorithms :
4.Timing Error Feedback Systems at Symbol Rate
Systematic Derivation of Synchronization Algorithms
First of all it should be mentioned that performance criterion for this derivation is the
ML .In fact the systematic derivation of ML synchronizers is straightforward only thing
must be done is averaging the likelihood function over the unwanted parameters:
i.e.:
Joint estimation of (θ, ε) :
Phase estimation:
Timing estimation:
But it is not possible to perform these averaging operations in closed form exception of a few cases, then approximation techniques must be used and so various algorithms result from the applying these techniques which can be systematic or not. In general synchronizers categorized into two main class: 1. Class DD/DA:Decision-directed(DD) or data-aided(DA) 2. Class NDA:Non-data-aided (NDA) Also can be further categorized according to how the timing/phase
estimates are extracted from the received signal,from this point of view two types is distinguishable: 1. Feedforward (FF) in which the estimate is derived from the received signal
before it is corrected in the interpolator (for timing) or the phase rotator (for
carrier recovery). 2. Feedback (FB) which derive an estimate of the error and feed a corrective signal back to the interpolator or phase rotator. In fact feedbacks inherently are capable to automatically track slowly varying paraneter changes. With this prelude proceed the main problem, With assumption using Nyquist pulses and a prefilter |F(ω)| being symmetric about 1/2Ts,demonstrated the likelihood function is simplified into following form : (Digital Communication Receivers: Synchronization, Channel Estimation, and Signal Processing Book , Heinrich Meyr, Marc Moeneclaey, Stefan A. Fechtel [1] p.268,269)
zn(ε)=z(nT+εT).
As said earlier suitable approximations must be found to remove the undesirable
parameters , if L(θ) is result of these approximation our problem is confined to find
the extermum of L(θ) in which θ is the set of paeameters are to be estimated so:
L(θ) is called objective function.
In [1] (chapter 4) is shown that :is independent of the synchronization parameter in fact for sufficiently large N
is approximated by its expected value due to the Law of Large Numbers ,as a consequence we should maximize the following objective function:
(1) In most digital receivers timing recovery is done prior to phase recovery. The reason
becomes clear by inspection of (1). since provided timing is known, one sample
per symbol of the matched filter output is sufficient for carrier phase estimation and symbol detection. To minimize the computational load in the receiver, carrier
phase estimation and correction must be made at the lowest sampling rate possible,
which is the symbol rate l/T. While the number of different carrier phase estimation algorithms is small,
there exists a much larger variety of digital algorithms for timing recovery. This
is due to the fact that the number of degrees of freedom in deriving an algorithm
is much larger. Most importantly, the sampling rate l/Ts to compute zn(ε) can
be chosen independently of the symbol rate. Case study of some algorithms: 1. NDA Timing Parameter Estimation
3. DA(DD) Timing Parameter Estimation
4. Mueller and Müller Algorithm
shima_kheradmand@yahoo.com