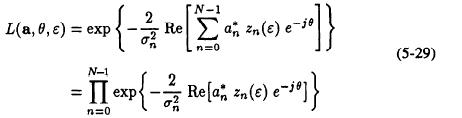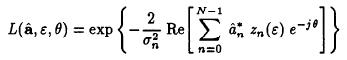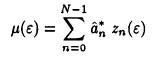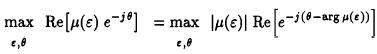Timing Recovery:

Introduction

2 Basic Functions for Digital Timing Recovery

Optimum ML Receivers

Derivation of Synchronization Algorithms:

1.NDA

2.NDA by Spectral Estimation

3.DA(DD)

4.Timing Error Feedback Systems at Symbol Rate

DA(DD) Timing Parameter Estimation

Replacing in eq. (5-29) the trial parameter an, and the phase θ by their
estimates yields a DD phase-independent algorithm:

 

This algorithm finds application when phase synchronization is done prior to
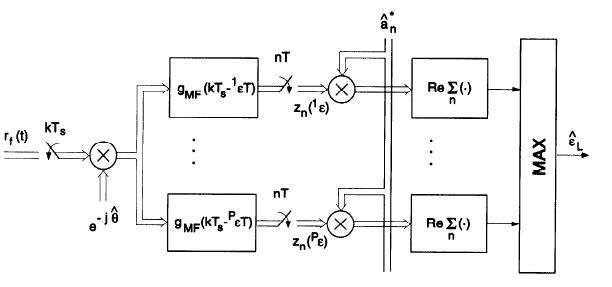
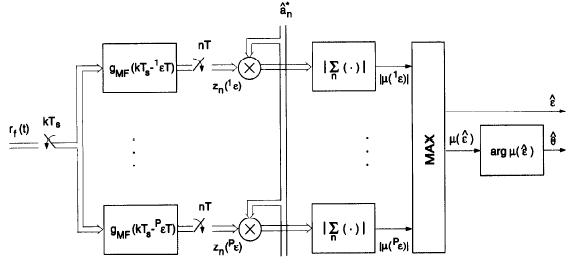
timing recovery. The computation of the objective function can again be computed in parallel. Instead of the nonlinearity to remove the data dependency we now have the multiplication by the symbols (seefollowing figure).

We next consider the joint estimation of (θ,ε):

The two-dimensional search over (0, e) can be reduced to a one-dimensional one by defining:

We then have:

 

The joint maximum is found by first maximizing the absolute value of μ(ε) (which is independent of θ). The second factor

is maximized to a value of one by θ = arg μ(ε). Hence, for timing estimation
we only need to maximize:

The carrier phase estimate 6 can then be computed directly as:

In a practical realization the summation is confined to L << N symbols.

 

 

home

shima_kheradmand@yahoo.com