Two Basic Functions for Digital Timing Recovery

In a digital receiver at first stage the signal is downconverted to (approximately)
baseband by multiplying it with the complex output of an osillator.The frequency 
oscillator is possibly controlled by a frequency control loop. The signal then enters 
an analog prefilter F(ω) before it is sampled and quantized. All subsequent signal
processing operations are performed digitally at the fixed processing rate of  l/Ts 
(or fractions of it) but we should remember that the digital receiver should have no
performance loss due to sampling and digital signal processing when compared to the 
analog counterpart.It seems if the condition of Sampling Theorem for Ts and
band-limited signal rf(t) is satisfied ,this problem is eliminated but we should be 
carefull since the noise samples {n(kTs)} , in general, are correlated,i.e.,statistically 
dependent that is the information carried by them must be taken into account which is
demonstrated under sufficient conditions on the design of the analog prefilter F(ω)
the samples rf(kTs) are sufficient statistics.Hence we continue with this assumption
that these samples contain all information.

In truly digital timing recovery  there exists only clock ticks at t = kTs,
incommensurate with the symbol rate l/T. The shifted samples must be 
obtained from those asynchronous samples {r(kTs)} solely by an algorithm 
operating on these samples (rather than shifting a physical clock).
The entire operation of digital timing recovery is best understood by emphasizing
that the only time scale available at the receiver is defined by units of Ts
and, therefore, the transmitter time scale defined by units of T must be expressed
in terms of units of Ts.
Since we need samples of the matched filter at (nT+εΤ), we should express 
this argument as follows: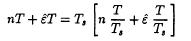

                                   
                                  

                                  
                             

The timing parameters (mn,μn) are uniquely defined given { ε0, Τ, Τs },In practice,
there is a block labled timing estimator which estimates { mn , μn } based on noisy 
samples of the received signal , therefore :
Digital timing recovery comprises two basic functions:
1-Estimation
The fractional time delay ε0 has to be estimated. The estimate  ε is used as
if it were the true value ε0 .
2-Interpolation and Decimation
From the samples {rf (kTs)} a set of samples (rf (kTs, + μnTs)} must be
computed. This operation is called interpolation and can be performed by a
digital, time-variant filter HI (exp(jTs) ,μnTs) .

Only the subset {y(mnTs))} = {z(nT + εT)} of values is required for further
processing. This operation is called decimation.

                        shima_kheradmand@yahoo.com